Łukasz Kocewiak

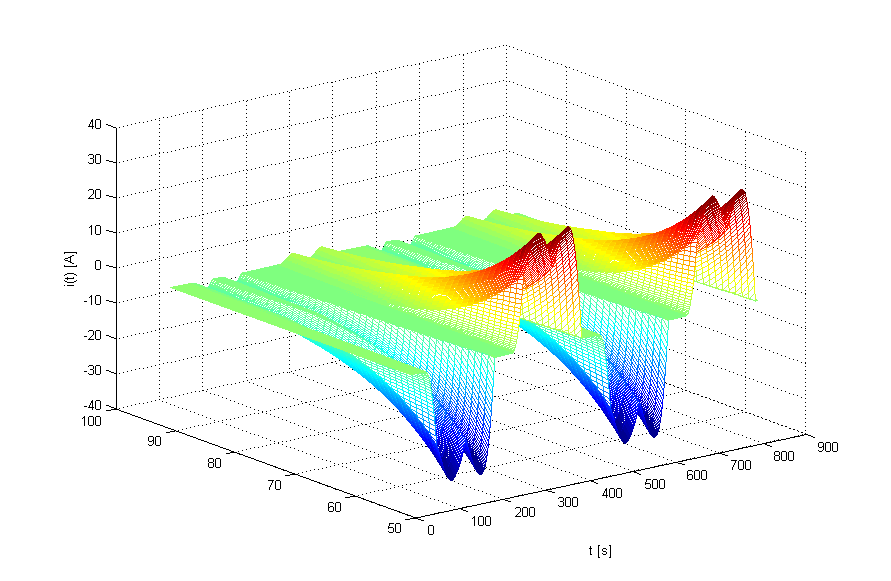
Converter setpoint adjustment

The power generation unit frequency response changes depending on an operating point, e.g. active power setpoint, voltage setpoint. That is important for stability analysis within lower frequency range where the influence of phase-locked loop and controllers with lower dynamics, e.g. voltage control, is visible. Combination of specific setpoints and grid impedances, especially in case of low short-circuit ratio, can trigger unwanted instability. One can perform mapping of different operational points and schedule only the one not leading to any oscillatory behaviour. This mitigation measure can be applied within the design phase and during power plant operation. However, it is rather considered as corrective mitigation measure when any hardware changes are not available.

Converter control adjustment

Controller parameter tuning, digital delay compensation and pulse-width modulation filter resonance damping (or shifting) methods can be applied to improve the inherent stable operating region, all of which are digital modification that can be rapidly applied mostly without modification of hardware. Controller can be adapted (e.g. loop gain reduction, impedance shaping) to local grid conditions during all phases of the asset lifecycle, i.e. design, commissioning, operation, thus can be considered as preventive as well as corrective instability mitigation measure. However, much more flexibility in controller parameters adjustment as well as control structure modification is possible during the design phase. Adaptive control where the parameters are changed on the fly is also an attractive option, however complex to implement.

Internal and external operational scenario adjustment

Control interactions can often be avoided by changing the electrical topology. A change of the power plant internal electrical infrastructure will affect the short-circuit power and / or shift the resonance points in the system. Avoiding specific contingency operation cases can maintain the short-circuit ratio at a satisfactory high level. Moreover, if the outcome of the analysis demonstrates that a hazardous resonance point can be avoided in a specific power plant electrical infrastructure configuration, then this grid topology can be considered as an intermediate or final mitigation measure. The operational measures can only be chosen according to the individual situation and will always be very specific. Adjustment of operational scenarios within the power plant is rather considered as corrective mitigation measure, however, can be applied also during the design phase as a preventive measure.

All electrical components and subsystems are interconnected within the entire power system and contribute to a certain degree to assure stable operation. Thus, operational scenarios may not be changed only within the power plant internal electrical infrastructure but also within the power system to which it is connected. That also includes neighbouring power plants. In many cases the transmission system operator has much more flexibility to define operational philosophy focused on maximizing fault infeed and avoiding unwanted resonances, thus consequently improve the entire system robustness. Adjustment of operational scenarios within the grid is rather considered as corrective mitigation measure to address grid expansion or connection of new power plants. One of possible mitigation measures applied within the power system is inter-tripping to avoid contingency scenarios leading to converter instability.

Additional passive filter

Contrary to described earlier operational measures and control adjustment, a high-voltage passive filter can be added to alter the resonance frequency of the power grid at the point of interest. There is a large variety of passive filters being able to improve damping within harmonic frequency range. Installation of a passive filter is considered as preventive mitigation measure. It is much easier to add the passive filter during the design phase. Moreover, passive filters provide extra damping which together with stability enhancement can also reduce transient overvoltage and harmonics within specified frequency range.

Additional active power electronic equipment

The control interaction is a phenomenon caused by the active participation of power generation unit converters, which can occur with e.g. purely damped plant, weak grid, resonant network. This is because the converter control loops play an important role in defining the overall impedance of power plant. The impedance of each power plant can be reshaped by the addition of supplementary shunt-connected converters, such as a static synchronous compensators to provide extra resistive damping at the hazardous resonance frequency via a damping controller. As this type of mitigation requires additional equipment it is considered as preventive mitigation measure. However, static synchronous compensator are more often installed with renewable-based power plants and additional damping can be provided on already existing assets, thus in that case active damper one can consider also as corrective instability mitigation technique. Moreover, active damper control scheme can be adjusted on already operating assets to address potential power grid topology changes.

Power system voltage stiffness increase

In conventional power systems characterized by extensive use of synchronous machines the short-circuit ratio is typically calculated to measure the strength of the grid to which converter-based power plant is connected. Any attempt to improve short-circuit ratio by increasing the fault level at the power plant point of common coupling can improve the stability. It can be achieved by (i) avoiding severe contingency operation, (ii) improving transmission system capabilities by adding e.g. extra lines, (iii) installing synchronous condensers characterized by short-circuit current contribution. Increasing the fault level can improve the system robustness within the low-frequency range as it reflects the system impedance at the fundamental frequency. This mitigation measure is preventive because can be much easier initiated during the planning and design phases. Due to the complexity in power system modifications to improve short-circuit ratio, it is difficult to think about it as a corrective measure, unless one could easy avoid severe contingency operation leading to low short-circuit ratio. For modern power systems characterized by extensive use of power electronic equipment the voltage stiffness increase can be achieved by dedicated control loops if grid-following converters or use of grid-forming converters to improve the stability.