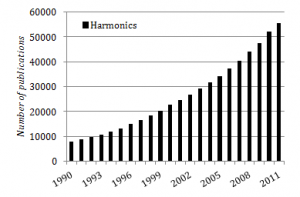
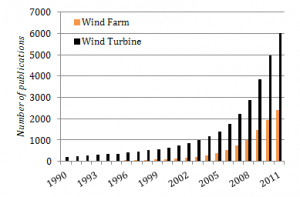
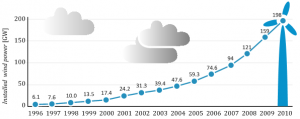
Ideally, an electrical power system in every certain point should show a perfectly sinusoidal voltage signal. However, it is difficult to preserve such desirable conditions. The deviation of the voltage and current waveforms from sinusoidal is described in terms of the waveform distortion, often expressed as harmonic distortion.
Harmonics are created when nonlinear loads draw nonsinusoidal current from a sinusoidal voltage source or are generated by purpose by active components. Harmonic distortion is caused by nonlinear devices in the power system where driven frequency is the power system fundamental component fo. A nonlinear device is one in which the current is not proportional to the applied voltage. While the applied voltage is perfectly sinusoidal, the resulting current is distorted.
According to definition commonly used in power system studies [1] characteristic harmonic exist when analyzed three-phase electrical system is considered to be balanced, the voltages and currents waveforms have identical shape and current and voltage are separated by exactly ±1/3 of the fundamental period. In such case zero sequence harmonics are for orders n=3m where m=1,2,3,... , positive sequence harmonics are for orders n=3m-2 and negative sequence harmonics are for orders n=3m-1.
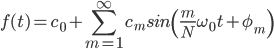
The harmonic emission of power electronic components can be categorized in characteristic and non-characteristic harmonics. The characteristic harmonic emissions are determined by the converter topology and the switching pattern applied. For instance, a typical configuration is a two-level, three-phase voltage source converter with sinusoidal pulse-width modulation. The modulation frequency ratio mf is defined as the switching frequency fc divided by the power system fundamental frequency fo. In double-edge naturally sampled pulse-width modulation significant sideband harmonics in this carrier group will occur at frequencies of ωct±2ωot, ωct±4ωot. And for the second carrier group, the significant sideband harmonics will occur at 2ωct±ωot, 2ωct±5ωot, 2ωct±7ωot. All triple sideband harmonics (e.g. 2ωct±3ωot, etc.) are canceled between legs because the phase angles of these harmonics rotate by multiples of 2π for all phase legs (i.e. common mode signals). [2], [3].

where Amn and Bmn are the Fourier coefficients.
Non-characteristic harmonics are not related to the converter topology, but are determined by the operating point and control scenario of the individual converter. Therefore, these are weakly correlated or even completely uncorrelated between different wind turbine generators [4].
Typical device with another driven frequency than fundamental component in the power system is voltage source converter with pulse width modulation which can be seen in nowadays wind turbines. If such converter is a grid-connected device the frequency components generated by it are dependent on both the power system fundamental component (i.e. modulated signal) and the carrier signal fundamental component (i.e. modulating signal). In this particular case harmonic components generated by the voltage source converter can be integer multiple of grid frequency, carrier frequency or a mixture of both of them.
Therefore in power systems where there is more than one driven frequency it is not straight forward to identify harmonic components and their origin. In fact the only occurrence of integer multiple frequencies of the power system fundamental frequency is the trivial case where a single sinusoid interacts with itself or its own harmonics. This situation was popular in the past when power systems comprised only passive components and synchronously rotating generators. Nowadays broadly used in modern power systems advanced power electronics contains also its own driven frequencies (not always equal or multiple integer of the power system frequency) which can affect generation of harmonic components of frequencies constituting a mixture of different driven frequencies.
[1] N. R. Watson and J. Arrillaga, Power System Harmonics. Wiley and Sons, 2003.
[2] N. Mohan, T. M. Undeland, and W. P. Robbins, Power electronics: Converters, Applications, and Design, 3rd ed. New York: Wiley and Sons, 2003.
[3] D. G. Holmes and T. A. Lipo, Pulse Width Modulation for Power Converters: Principles and Practice. IEEE Press, 2003.
[4] J. Verboomen, R. L. Hendriks, Y. Lu, and R. Voelzk, "Summation of Non-Characteristic Harmonics in Wind Parks," in Proc. Nordic Wind Power Conference, Bornholm, 2009.