I would like to mention at the begging that for more than last three years I have been working on various aspects of harmonic in power system and power electronics. Almost all of my research activities were focused mainly on the application of harmonic analysis in large offshore wind farms. Since I started there have been few observations and ideas that I would like to share with you. From my perspective such knowledge sharing approach can bring closer harmonic analysis in electrical engineering and allow to establish a dialog between engineers and physicians from different fields of science. Let me start from the historical background of harmonic analysis.
First well documented appearance of harmonics in relation to mathematics and science is from ancient Greek. The science which pursued the investigation of multiple and epimoric (ratios of the form [n+1]:n) ratios in music was concerned with the mathematical 'fitting-together' (harmonia) of the constituent notes and intervals of music [1].
Harmonics were described by Claudius Ptolemy, who related musical harmonies to the properties of mathematical proportions derived from the production of sounds themselves. Ptolemy argued for basing musical intervals on mathematical ratios, in agreement with the followers of Pythagoras, backed up by empirical observation. Ptolemy wrote about how musical notes could be translated into mathematical equations and vice versa [2]. Those harmonies he considered to be distributed in all aspects of the physical universe. In particular, they were there in the phenomena of the planets and the human soul [3].
Nowadays, harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms, mathematical tools significantly useful in different areas of engineering. The basic waves are called harmonics, but the name harmonic in this context is generalized beyond its original meaning of integer frequency multiples.
It can be said that the beginning of nowadays harmonic analysis reaches back a French mathematician and physicist, Joseph Fourier, who originally defined the Fourier series for real-valued functions of real arguments, and using the sine and cosine functions as the basis set for the decomposition. Fourier series could be used only for analysis of periodic functions.
Many different approaches of defining and understanding the concept of Fourier series have been developed since that time. All are consistent with one another, but each of which emphasizes different aspects of the topic simultaneously extending significantly the basic concept of harmonic analysis. Some of the more powerful and elegant approaches based on mathematical ideas and tools not available at the Fourier time extended his original work and are successfully applied in harmonic analysis at present.
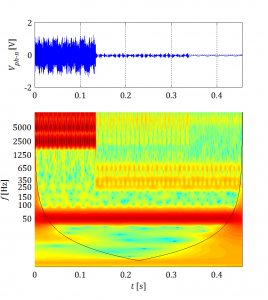
Many other Fourier-related transforms (e.g. Laplace transform, Fourier transform, short-time Fourier transform, wavelet transform) have since been defined, extending the initial idea to other applications. This general area of inquiry is now by physicists and engineers called harmonic analysis.
I hope this short introduction appears to be interesting for you and can encourage you to check later posts regarding various aspects of harmonic studies in engineering and large offshore wind farms. If you have any questions or comments do not hesitate to drop me a line below.
[1] D. Creese, Monochord in Ancient Greek Harmonic Science. Cambridge University Press, 2010.
[2] J. Solomon, Ptolemy Harmonics: Translation and Commentary. Brill Academic Publishers, 1999.
[3] A. Barker, Scientific Method in Ptolemy's Harmonics. Cambridge University Press, 2001.
One reply on “Harmonic analysis - historical background”
Thank you for nice explaination